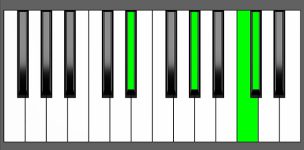
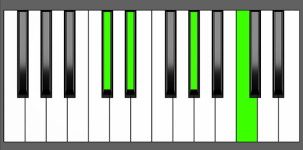
Piano Diagram of G# add11 in Root Position

The G# add11 chord is a G# Major (G#, B#, D#) with an extra 11th note (C#). It’s an added tone chord, meaning that it’s built by adding an extra interval to a triad. Keep reading to gain a deeper understanding of the music theory behind this chord.
Structure of G# add11
Notes |
|---|
| G#, B#, D#, C# |
Intervals |
|---|
| R, 3, 5, 11 |
Playing Extended Chords on Piano
Extended chords are challenging to play in their entirety on the piano due to the high number of notes involved, or the wide intervals between them like in the case of add 11th chords.
To simplify these chords, pianists may omit certain notes, typically the root or fifth, or divide the chord between both hands.
G# add11 Chord Inversions
G# add11 chord has a total of 3 inversions:
| Root Position: | G# | B# | D# | C# |
| 1st Inversion: | B# | D# | G# | C# |
| 2nd Inversion: | D# | G# | B# | C# |
| 3rd Inversion: | C# | D# | G# | B# |
Piano Keyboard Diagrams
Chord Inversions on Piano
Chord inversions are a crucial concept in music theory as they allow for a greater understanding of how chords are constructed and how they can be used in progressions.
However, it’s important to note that the diagrams depicting the sequence of notes in a chord inversion on a piano keyboard may not always translate to practical playing. This is because proper chord voicings involve distributing the notes of the chord across different octaves and positions on the keyboard, which may differ from the basic shape of the chord’s inversions.
Therefore, while chord inversion diagrams help understand the structure and sequence of notes in a chord, they may not always be the most efficient way to play the chord on a piano keyboard.
Music Theory and Harmony of G# add11
Building the G# add11 Chord: Different Approaches
Starting from the G# Major Scale:
To build an add11 chord, you can use the Major scale as a reference by combining a Root, a 3rd, a 5th, and an 11th.


Apply the formula R, 3, 5, 11 to get a G# add11 chord.
- Begin with the Root note, G#.
- Select the 3rd note, B#.
- Add the 5th note, D#.
- Finally, include the 11th note, C#, which is a 4th note but an octave higher.
by Combining Intervals:
To build an add11 chord, one approach is to combine specific intervals, namely a major 3rd, a minor 3rd, and a minor 7th.
3 + m3 + m7 = add11 Chords
For example, to make the G# add11 chord, you can stack
- G#-B# (major 3rd),
- B#-D# (minor 3rd),
- and D#-C# (minor 7th) on top of each other.
How to Use G# add11 in a Chord Progression
Music theory classifies chords based on their harmonic function, which can be categorized as either tonic, subdominant, or dominant chords. The G# add11 chord, which can replace a regular G# major chord, can have any of these functions, depending on its context in a composition
However, the 11th note (C#) present in G# add11 may not always fit with the scale being used. This means that the chord can introduce a non-diatonic tone that does not belong to either the D# major or B# minor scales.
For this reason, the use of the G# add11 chord in these keys should be approached with caution to avoid dissonance or unintended clashes with the melody or the bass line. The use of non-diatonic chords should be intentional and targeted to specific musical effects.
The G# add11 chord can serve as a tonic chord that resolves the tension created by a preceding dominant chord, such as D#7. Alternatively, in a chord progression in the key of C# major, it can also act as a dominant chord. In both cases, it’s common to use the add11 chord in chromatic or diatonic modulation. I will provide some examples of its use in chord progressions.
on Major Scales
Given that G# Maj7 and G#7 chords are predominantly found in theoretical keys, it is more practical to reference their equivalent keys:
| Major Scales | I | ii | iii | IV | V | vi | vii |
|---|---|---|---|---|---|---|---|
| G# = Ab | Ab Maj7 ⇒ Ab add11 = G# add11 |
Bb min7 | C min7 | Db Maj7 | Eb7 | F min7 | Gm7b5 |
| D# = Eb | Eb Maj7 | F min7 | G min7 | Ab Maj7 ⇒ Ab add11 = G# add11 | Bb7 | C min7 | Dm7b5 |
| C# | C# Maj7 | D# min7 | E# min7 | F# Maj7 | G#7 ⇒ G# add11 | A# min7 | B#m7b5 |
- Tonic chord in Ab Major as Ab add11
- Non-diatonic Subdominant chord in Eb Major as Ab add11
- Dominant chord in C# Major (less common)
on Natural minor Scales
| Minor Scales | i | ii | III | iv | v | VI | VII |
|---|---|---|---|---|---|---|---|
| E# = F | F min7 | Gm7b5 | Ab Maj7 ⇒ Ab add11 = G# add11 | Bb min7 | C min7 | Db Maj7 | Eb7 |
| B# = C | C min7 | Dm7b5 | Eb Maj7 | F min7 | G min7 | Ab Maj7 ⇒ Ab add11 = G# add11 | Bb7 |
| A# | A# min7 | B#m7b5 | C# Maj7 | D# min7 | E# min7 | F# Maj7 | G#7 ⇒ G# add11 |
- Mediant chord in F minor as Ab add11
- Non-diatonic Submediant chord in C minor as Ab add11
- Dominant chord in A# minor (less common)
G# add11 in G# Major
G# add11 in D# Major (Non-Diatonic)
G# add11 in C# Major
Another way to use the G# add11 chord is as a variation of the dominant chord in the C# major scale.
In this case, the G# add11 chord functions as a variation of the G# Major 7 chord, serving as the fifth degree of the C# major scale. When used in a ii-V-I progression, the G# add11 chord on the fifth degree can function as the dominant chord that resolves to the first degree.
While this may not be the most ideal use of the chord, as the 11th corresponds with the root of the first degree, it is still worth mentioning as a possible variation.
| I | ii | iii | IV | V | vi | vii |
| C# Maj7 | D# min7 | E# min7 | F# Maj7 | G#7 ⇒ G# add11 | A# min7 | B#m7b5 |
G# add11 as V degree – Chord Progressions
You can try playing these chord progressions to hear how the G# add11 chord works as a substitute for the subdominant (IV degree) in a chord progression:
ii V I
| ii | V | I |
| D# min7 | G# add11 | G#7 | C# Maj7 |
I IV V
| I | IV | V |
| C# Maj7 | F# Maj7 | G# add11 | G#7 |
I V vi IV
| I | V | vi | IV |
| C# Maj7 | G# add11 | G#7 | A# min7 | F# Maj7 |
I IV vi V
| I | IV | vi | V |
| C# Maj7 | F# Maj7 | A# min 7 | G# add11 | G#7 |
I IV ii V iii vi ii V
| I | IV | ii | V | iii | vi | ii | V |
| C# Maj7 | F# Maj7 | D# min7 | G# add11 | G#7 | E# min7 | A# min7 | D# min7 | G# add11 | G#7 |
G# add11 in E# minor
G# add11 in B# minor (Non-Diatonic)
G# add11 in A# minor
Another way to use the G# add11 chord is as a substitution for the leading tone chord in the key of A# minor. In this context, the G# add11 chord functions as a variation of the G#7 chord, serving as the VII degree.
| i | ii | III | iv | v | VI | VII |
| A# min7 | B#m7b5 | C# Maj7 | D# min7 | E# min7 | F# Maj7 | G#7 ⇒ G# add11 |
G# add11 as VII degree – Chord Progressions
You can try playing these chord progressions to hear how a G# add11 works as a substitute for the leading tone in a chord progression:
i VI VII
| i | V | VII |
| A# min7 | F# Maj7 | G# add11 | G#7 |
i v VI VII
| i | v | VI | VII |
| A# min7 | E# min7 | F# Maj7 | G# add11 | G#7 |
i III VII VI
| i | III | VII | VI |
| A# min7 | C# Maj7 | G# add11 | G#7 | F# Maj7 |
Circle Progression
| i | iv | VII | III | VI | ii | V7 | i |
| A# min7 | D# min7 | G# add11 | G#7 | C# Maj7 | F# Maj7 | B#m7b5 | E#7 | A# min7 |
Chord Similarities
add11 and sus4 Chords
Add11 and sus4 chords share many similarities, as they both contain similar sets of notes, with the only difference being the presence or absence of the 3rd note and the location of the 4th note. The add11 chord includes
- the root,
- 3rd,
- 5th,
- and an 11th note played at a higher octave,
while the sus4 chord includes
- the root,
- 4th,
- and 5th notes.
For example, a G# add11 chord consists of the notes G#, B#, D#, and C#, while a G# sus4 chord consists of the notes G#, C#, and D#.
The inclusion of the major 3rd note in the add11 chord provides stability to the chord, creating a less tense sound. In contrast, the sus4 chord creates a more suspended, unresolved sound due to the absence of the 3rd note. However, despite these differences, the two chords still share a similar sound.
add11 and add4 Chords
Although add11 chords and add4 chords share the same notes, it’s essential to note that even if they are the same note, a 4th is not the same as an 11th because there is an octave of difference between them. While this distinction may not be significant when playing an inversion of the chord, it’s still crucial to be aware of.
The Debate Around add2 and add4 Chords
In addition, there is some debate about the usefulness of add2 and add4 chords as distinct entities. Add2 chords are made by the Root, the 2nd, the 3rd, and the 5th, while add4 chords are made by the Root, the 3rd, the 4th, and the 5th. Because these chords create a cluster of notes, their root position can sound pretty dissonant.
Playing the 2nd or 4th note at a higher octave can help to reduce the dissonant cluster of notes created by add2 and add4 chords. For this reason, a better way to formulate these chords is by using add9 and add11 chords, which provide a more harmonically pleasing sound while still incorporating the desired note.
Furthermore, if we really need to add a 2nd or a 4th note, then we should take care to omit the 3rd, which is exactly what suspended chords (sus2 and sus4) are designed to do.
Alternative Names for G# add11
It’s important to note that G#11 and G# add11 are not the same chord. When building 11th chords, there are a minor 7th and a 9th in addition to the 11th interval.
- G# add11
- Sol# add11
- G# add(11)
- G# (add11)
- G# add11th