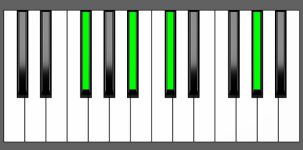
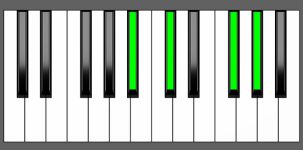
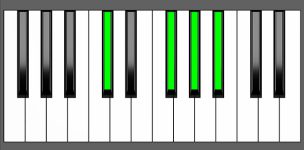
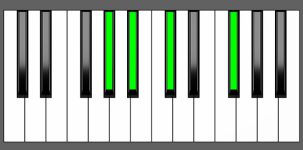
Piano Diagram of Gb add9 in Root Position

To form a Gb add9 chord, you simply include a 9th note (Ab) to a Gb Major chord (Gb, Bb, Db). Such chords are referred to as added tone chords as they involve the addition of supplementary intervals to a triad. The Gb add9 chord is distinct from the Gb9 chord because it doesn’t have a 7th, whereas the Gb9 chord includes the 7th note. Continue reading to discover additional information about the fundamentals of added tone chords and their applications in music.
Structure of Gb add9
Notes |
|---|
| Gb, Bb, Db, Ab |
Intervals |
|---|
| R, 3, 5, 9 |
Playing Extended Chords on Piano
Extended chords can be difficult to play in their entirety on the piano due to the large number of notes involved or the distance between intervals like in this case. To simplify these chords, pianists often omit certain notes (usually the Root or the fifth) or split the chord between both hands. However, even with these simplifications, extended chords can create complex and dense harmonies, making voicing a challenging task.
Gb add9 Chord Inversions
Gb add9 chord has a total of 3 inversions:
| Root Position: | Gb | Bb | Db | Ab |
| 1st Inversion: | Bb | Db | Gb | Ab |
| 2nd Inversion: | Db | Gb | Ab | Bb |
| 3rd Inversion: | Ab | Bb | Db | Gb |
Piano Keyboard Diagrams
Chord Inversions on Piano
Chord inversions are a crucial concept in music theory as they allow for a greater understanding of how chords are constructed and how they can be used in progressions.
However, it’s important to note that the diagrams depicting the sequence of notes in a chord inversion on a piano keyboard may not always translate to practical playing.
This is because proper chord voicings involve distributing the notes of the chord across different octaves and positions on the keyboard, which may differ from the basic shape of the chord’s inversions.
Music Theory and Harmony of Gb Add9
Building the Gb add9 Chord: Different Approaches
Starting from the Gb Major Scale:
To build an Add 9 chord, begin by using the Major scale as a reference and selecting the Root, 3rd, 5th, and 9th notes.


Here are the steps to get the Gb add9 chord using the formula R, 3, 5, 9:
- Begin with the Root note, which is Gb.
- Add the 3rd note, which is Bb.
- Include the 5th note, which is Db.
- Finally, add the 9th note, which is Ab.
by Combining Intervals:
Another approach to building an Add 9 chord involves combining particular intervals, such as a major 3rd, minor 3rd, and perfect 5th.
3 + m3 + 5 = add9 chords
For example, to create a Gb add9 chord, you can layer
- Gb-Bb (a major 3rd),
- Bb-Db (a minor 3rd),
- and Db-Ab (a perfect 5th) on top of each other.
How to Use Gb add9 in a Chord Progression
In music theory, the concept of harmonic function refers to the role a chord plays in a musical composition. A stable harmonic function is associated with a chord that provides a sense of rest or resolution, while a dominant harmonic function creates a sense of tension or instability that often leads to a resolution to a stable chord.
The harmonic function of a Gb add9 chord is not fixed and can vary based on the surrounding harmonic context and the musical composition. For instance, when a Gb add9 chord follows a dominant chord like Db7, it functions as a stable chord that resolves the preceding tension.
However, in other situations, such as in a chord progression in the key of Cb major, the Gb add9 chord can serve as a dominant chord.
It is helpful to explore which scales and degrees include a Gb Maj7 or Gb7 chord, which can potentially be substituted with a Gb add9 chord.
on Major Scales
| Major Scales | I | ii | iii | IV | V | vi | vii |
|---|---|---|---|---|---|---|---|
| Gb | Gb Maj7 ⇒ Gb add9 | Ab min7 | Bb min7 | Cb Maj7 | Db7 | Eb min7 | Fm7b5 |
| Db | Db Maj7 | Eb min7 | F min7 | Gb Maj7 ⇒ Gb add9 | Ab7 | Bb min7 | Cm7b5 |
| Cb = B | B Maj7 | C# min7 | D# min7 | E Maj7 | F#7 ⇒ F# add9 = Gb add9 | G# min7 | A#m7b5 |
- Tonic chord in Gb Major
- Subdominant chord in Db Major
- Dominant chord in B Major as F# add9
on Natural minor Scales
| Minor Scales | i | ii | III | iv | v | VI | VII |
|---|---|---|---|---|---|---|---|
| Eb | Eb min7 | Fm7b5 | Gb Maj7 ⇒ Gb add9 | Ab min7 | Bb min7 | Cb Maj7 | Db7 |
| Bb | Bb min7 | Cm7b5 | Db Maj7 | Eb min7 | F min7 | Gb Maj7 ⇒ Gb add9 | Ab7 |
| Ab | Ab min7 | Bbm7b5 | Cb Maj7 | Db min7 | Eb min7 | Fb Maj7 | Gb7 ⇒ Gb add9 |
- Mediant chord in Eb minor
- Submediant chord in Bb minor
- Leading tone chord in Ab minor
Gb add9 Chord Function in Major and Minor Keys
Understanding Scale Degrees
When harmonizing a scale, you create chords using the notes from that scale. Each note in the scale is assigned a degree, reflecting its position in the scale. In the diatonic major scale, the degrees are as follows:
- Tonic: This is the first degree of the scale and provides a stable tonal center. It’s often referred to as the “home base” of the music.
- Supertonic: This is the second degree of the scale and is frequently used as a passing note between the tonic and other scale degrees.
- Mediant: This is the third degree of the scale and helps to establish whether the scale is major or minor. It’s located halfway between the tonic and dominant notes.
- Subdominant: This is the fourth degree of the scale and is often used as a complementary harmony to the dominant.
- Dominant: This is the fifth degree of the scale and generates tension and a sense of expectation. It’s typically resolved by returning to the tonic.
- Submediant: This is the sixth degree of the scale and is often utilized as a transition between the dominant and tonic.
- Leading tone: This is the seventh degree of the scale and is located one half-step below the tonic. It produces a strong sense of tension and a desire to resolve to the tonic.
Understanding the scale degrees is important for creating chords and understanding how they relate harmonically to each other.
Gb add9 in Gb Major
You can use a Gb add9 chord as a substitution for the Gb major or Gb major 7th chord, which is the first chord in the harmonized Gb major scale.
In a major key, the first chord (I chord) built on the first degree of the major scale serves as the tonic chord, creating the harmonic center of the chord progression.
| I | ii | iii | IV | V | vi | vii |
| Gb Maj7 ⇒ Gb add9 | Ab min7 | Bb min7 | Cb Maj7 | Db7 | Eb min7 | Fm7b5 |
Gb add9 Chord Progressions as I degree
Incorporating an add9 chord in your music can add an element of intrigue and variation. It can be used as a substitute for a traditional major chord or as a modulation towards a more stable Gb Major chord. For instance, try using the Gb add9 chord as the first chord in a progression and see how it affects the overall sound.
ii V I
| ii | V | I |
| Ab min7 | Db7 | Gb add9 | Gb Maj7 |
I IV V
| I | IV | V |
| Gb add9 | Gb Maj7 | Cb Maj7 | Db7 |
I V vi IV
| I | V | vi | IV |
| Gb add9 | Gb Maj7 | Db7 | Eb min7 | Cb Maj7 |
I IV vi V
| I | IV | vi | V |
| Gb add9 | Gb Maj7 | Cb Maj7 | Eb min7 | Db7 |
Gb add9 in Db Major
You can also use the Gb add9 chord as a substitute for the Gb major 7th chord when it appears on the fourth degree of the Db major scale. This substitution can be employed in the I-IV-V chord progression, with the add9 chord on the fourth degree acting as a transitional chord between the first and fifth degrees.
| I | ii | iii | IV | V | vi | vii |
| Db Maj7 | Eb min7 | F min7 | Gb Maj7 ⇒ Gb add9 | Ab7 | Bb min7 | Cm7b5 |
Gb add9 as IV degree – Chord Progressions
Try experimenting with chord progressions that use a Gb add9 chord instead of the typical Gb Maj7 chord on the fourth degree in the Db major scale. This substitution can add some variety and interest to the common I-IV-V progression, where the add9 chord can act as a transitional chord between the first and fifth degrees.
I IV V
| I | IV | V |
| Db Maj7 | Gb add9 | Gb Maj7 | Ab7 |
I V vi IV
| I | V | vi | IV |
| Db Maj7 | Ab7 | Bb min7 | Gb add9 | Gb Maj7 |
I IV vi V
| I | IV | vi | V |
| Db Maj7 | Gb add9 | Gb Maj7 | Bb min7 | Ab7 |
Gb add9 in Cb Major
Gb add9 in Eb minor
In the key of Eb minor, you can use the Gb add9 chord as a substitution for the Gb Maj7 chord, which serves as the third degree in the scale.
| i | ii | III | iv | v | VI | VII |
| Eb min7 | Fm7b5 | Gb Maj7 ⇒ Gb add9 | Ab min7 | Bb min7 | Cb Maj7 | Db7 |
Gb add9 as III degree – Chord Progressions
The following chord progressions showcase how the Gb add9 chord can be used as a variation of the mediant (III degree) chord.
i III
| i | III |
| Eb min7 | Gb add9 | Gb Maj7 |
i III VII VI
| i | III | VII | VI |
| Eb min7 | Gb add9 | Gb Maj7 | Db7 | Cb Maj7 |
Circle Progression
| i | iv | VII | III | VI | vii | V7 | i |
| Eb min7 | Ab min7 | Db7 | Gb add9 | Gb Maj7 | Cb Maj7 | Fm7b5 | Bb7 | Eb min7 |
(A progression that follows the circle of fifths is a sequence of chords that move in ascending or descending fifths from one key to another. It’s called a “circle” progression because if you keep moving through the sequence, you’ll eventually come back to the starting point, creating a “circle” of keys.)
Gb add9 in Bb minor
In the key of Bb minor, the add9 chord can also be used as a substitution for the chord on the sixth degree, which is Gbmaj7.
| i | ii | III | iv | v | VI | VII |
| Bb min7 | Cm7b5 | Db Maj7 | Eb min7 | F min7 | Gb Maj7 ⇒ Gb add9 | Ab7 |
Gb add9 as VI degree – Chord Progressions
To better understand how the add9 chord can be used as a substitute for the Gb Maj7 chord when it functions as the submediant (VI degree) in a Bb minor scale, you can experiment with the following chord progressions:
i VI VII
| i | VI | VII |
| Bb min7 | Gb add9 | Gb Maj7 | Ab7 |
i v VI VII
| i | v | VI | VII |
| Bb min7 | F min7 | Gb add9 | Gb Maj7 | Ab7 |
i III VII VI
| i | III | VII | VI |
| Bb min7 | Db Maj7 | Ab7 | Gb add9 | Gb Maj7 |
Gb add9 in Ab minor
Another way to use the Gb add9 chord is as a substitution for the leading tone chord in the key of Ab minor. In this context, the Gb add9 chord functions as a variation of the Gb7 chord, serving as the VII degree of the Ab minor scale.
| i | ii | III | iv | v | VI | VII |
| Ab min7 | Bbm7b5 | Cb Maj7 | Db min7 | Eb min7 | Fb Maj7 | Gb7 ⇒ Gb add9 |
Gb add9 as VII degree – Chord Progressions
Play the following chords to hear how the Gb add9 works as a substitution for the leading tone (VII degree) in a chord progression.
I suggest playing the first inversion of Ab min7 (Cb, Eb, Gb, Ab), the second inversion of Fb Maj7 (Cb, Eb, Fb, Ab), and the root position of Gb add9 (Gb, Bb, Db, Ab).
By using these chords, the highest note in each chord will be an Ab, which creates a consistent and stable sound. Then, you can transition from the Gb add9 chord to a Gb major chord by simply moving the ninth (Ab) down to a Gb note.
i VI VII
| i | V | VII |
| Ab min7 | Fb Maj7 | Gb add9 | Gb7 |
i v VI VII
| i | v | VI | VII |
| Ab min7 | Eb min7 | Fb Maj7 | Gb add9 | Gb7 |
i III VII VI
| i | III | VII | VI |
| Ab min7 | Cb Maj7 | Gb add9 | Gb7 | Fb Maj7 |
Add9 and Add2 Chords: Similarities and Differences
Add9 and add2 chords are similar in that they both contain the second note of the major scale as an additional note to the basic triad. However, the difference between the two is that the add9 chord includes the second note an octave higher, whereas the add2 chord includes the second note as it is in the scale.
The Debate Around Add2 and Add4 Chords
There is some debate about the usefulness of add2 and add4 chords as distinct entities.
Add2 chords are made by:
- the Root,
- the 2nd,
- the 3rd,
- and the 5th,
while add4 chords are made by:
- the Root,
- the 3rd,
- the 4th
- and the 5th.
These chords can sound pretty dissonant in their root position due to the cluster of notes they create. However, playing the 2nd or 4th note at a higher octave can help reduce the dissonance.
To achieve a more harmonically pleasing sound, it’s better to use add9 and add11 chords, which still include the desired note.
If we really need to add a 2nd or 4th note, we should omit the 3rd, which is exactly what suspended chords (sus2 and sus4) are designed for.
Alternative Names for Gb add9 Chord
- Gb add9
- Solb add9
- Gb (add9)
- Gb add(9)
- Gb add 9th
Conclusion
The chord progressions and examples presented in this post provide a comprehensive overview of the most common uses of the Gb add9 chord. It’s important to note, however, that many advanced harmony-related topics could not be included due to space constraints. These topics include chord progressions built on harmonic and melodic scales, modal scales, hidden tonality, secondary dominants and other chord substitutions, non-functional harmony and atonal music, modal interchange and borrowed chords, voice leading and counterpoint, chromatisms, jazz harmony…I mean, music theory is a huge topic!
Although I couldn’t cover all of these topics in my post, I encourage readers to continue exploring these areas in their study and research. By expanding your knowledge in these advanced areas of music theory, you can gain a deeper understanding of the harmonic possibilities that exist beyond the basics presented here.