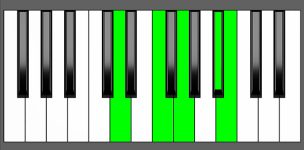
Piano Diagram of G7#9 in Root Position

A G7#9 chord is an altered dominant seventh chord that is built upon the key of G. This chord consists of the root G, the major third B, the perfect fifth D, the minor seventh F, and the sharp ninth A#. The G7#9 chord can be used as a substitute for dominant chords only in specific musical contexts. Keep reading to learn more about the music theory that underpins this chord.
Structure of G7#9
Notes |
|---|
| G, B, D, F, A# |
Intervals |
|---|
| R, 3, 5, m7, #9 |
How to play a G7#9
To play a G7#9 chord, you can use the following voicing: start by playing the root note G with your left hand. Then, with your right hand, play the notes B (major 3rd), F (minor 7th), and A# (sharp 9th).
G + B, F, A#
This approach will result in a simplified G7#9 chord that includes only the essential notes: the root note, major 3rd, minor 7th, and sharp 9th.
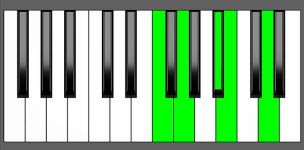
G7#9 Chord Inversions
The G7#9 chord has a total of 4 inversions:
| Root Position: | G | B | D | F | A# |
| 1st Inversion: | B | D | F | G | A# |
| 2nd Inversion: | D | F | G | A# | B |
| 3rd Inversion: | F | G | A# | B | D |
| 4th Inversion: | A# | B | D | F | G |
Piano Keyboard Diagrams

Chord Inversions on Piano
Having a solid understanding of chord inversions is a crucial element of music theory since it sheds light on how chords are constructed. When it comes to playing chord inversions on a piano, it’s essential to keep in mind that the charts and graphs depicting the order of notes may not always be feasible or even playable.
To achieve the proper chord voicings on a piano, you must spread the chord notes across various octaves and positions on the keyboard. This often entails deviating from the typical shape of the chord’s inversions shown in charts, which may not be the most practical or comfortable way to play the chord.
While chord inversion charts can help understand the structure and sequence of notes in a chord, it’s always a good idea to experiment with different voicings and fingerings to find the most efficient and comfortable way to play the chord, while still preserving its intended harmonic function and sound.
Music Theory and Harmony of G7#9
Dominant 7#9 chords are often referred to as the “Hendrix chord” due to their prominent use in songs like “Voodoo Child“, “Foxy Lady“, and “Purple Haze“. If you know these songs, then you can easily recall the distinct sound and mood of the 7#9 chord.
The G7#9 chord can replace or enhance the G7 chord, typically on the V degree, but also on the III degree, and occasionally on other degrees as a secondary dominant chord. However, it has a distinct funky vibe, so it should be used carefully in the appropriate musical context.
Before delving into the most frequent usage of this chord, let’s first understand how to construct it.
Building the G7#9 Chord: Different Approaches
Starting from the G Major Scale:
To form a 7#9 chord, you combine the root, the major 3rd, the 5th, the minor 7th, and the sharp 9th from a major scale.


To create a G7#9 chord, apply the formula R, 3, 5, m7, #9 in the following manner:
- Begin with the Root note, which is G.
- Select the major 3rd interval, which is B, and add it to the chord.
- Add the 5th interval, which is D.
- Add the minor 7th interval, F.
- Finally, select the 9th, A, and add a half tone to get the #9th, A#.
By following this simple formula, you can create a 7#9 chord from any major scale.
by Combining Intervals:
One method to create a 7#9 chord is by combining specific intervals – a major 3rd, a minor 3rd, and a perfect 4th.
3 + m3 + m3 + 4 = 7#9 Chords
For example, to build a G7#9 chord:
- we start with the root note G.
- We then add a major 3rd interval, which is four half-steps up from the root, to get B.
- Next, we add a minor 3rd interval, which is three half-steps up from B, to get D.
- Then, we add another minor 3rd so we find the minor 7th F and
- lastly, we add a perfect 4th interval, which is five half-steps up from F, to get A#.
Together, these intervals form the G7#9 chord.
How to Use G7#9 in a Chord Progression
The G7#9 can work as a substitute or as a passing chord to a G7 that can be found in major and natural minor scales. The 7#9 chord is considered a non-diatonic chord, which means that it contains notes that are not found in either the major or minor scales. Its unique sound is achieved by adding a sharp 9th interval (which is equivalent to a minor 3rd at the higher octave) to the dominant 7th chord, creating a dissonant yet interesting tonal color.
Most common uses of G7#9
G7#9 in C Major and C minor
The G7#9 chord is commonly used as a dominant chord. In the key of C major, the G7#9 chord can be used as the V7 chord, which leads back to the I chord (C major).
| Major Scale | I | ii | iii | IV | V | vi | vii |
|---|---|---|---|---|---|---|---|
| C | C Maj7 | D min7 | E min7 | F Maj7 | G7 ⇒ G7#9 | A min7 | Bm7b5 |
- Substitute or Passing Chord to the Dominant chord in C Major
G7#9 as Substitute for G min7
The G7 chord derived from the harmonic minor scale is commonly used to replace a G min7 chord in the key of C minor. In some cases, the G7#9 chord can also be used instead of the G7 chord, further enhancing the harmonic tension and leading to the C min7 chord.
| Minor Scale | i | ii | III | iv | v | VI | VII |
|---|---|---|---|---|---|---|---|
| C | C min7 | Dm7b5 | Eb Maj7 | F min7 | G min7 ⇒ G7 ⇒ G7#9 | Ab Maj7 | Bb7 |
- Substitute or Passing Chord to the Dominant chord in C minor
G7#9 in a I – III7 Progression
The G7#9 chord is often used as a substitution for the III degree in an I – III7 chord progression, which traditionally features a G minor chord. This chord progression, represented by the chords Eb Maj7 and G7, can accommodate the G7#9 chord in place of the expected G minor chord.
| Major Scale | I | ii | iii | IV | V | vi | vii |
|---|---|---|---|---|---|---|---|
| Eb | Eb Maj7 | F min7 | G min7 ⇒ G7 ⇒ G7#9 | Ab Maj7 | Bb7 | C min7 | Dm7b5 |
- Substitute or Passing Chord to the Mediant chord in Eb Major
G7#9 in A minor
While the G7#9 chord can be used in the key of A minor, it may not be the most common use of this chord. In fact, the resolution to A minor may be less strong than C major or C minor.
| Minor Scale | i | ii | III | iv | v | VI | VII |
|---|---|---|---|---|---|---|---|
| A | A min7 | Bm7b5 | C Maj7 | D min7 | E min7 | F Maj7 | G7 ⇒ G7#9 |
- Substitute or Passing Chord to the Leading Tone chord in A minor (less common)
G7#9 as Substitute for a Secondary Dominant 7th chord
A secondary dominant is a type of chord that is not in the main key of a musical piece but is used to create a strong pull towards another chord that is. In Western music, the fifth scale degree has a strong “dominant” function and creates tension that resolves to the first scale degree chord (I). A secondary dominant chord is used to create this same dominant function but towards a different chord, leading to a temporary departure from the main key.
For example, in the key of F major, the chord of C7 is the V chord and leads back to the I chord of F Maj7. Adding another chord between F Maj7 and C7 that creates a strong pull towards C7 creates a secondary dominant chord. In this case, using a G7 chord creates a pull towards C7, as G7 is the V chord in the key of C.
| F Maj7 | C7 |
⇒
| F Maj7 | G7 | C7 |
Instead of using a regular G7 chord, you can also use the G7#9 chord in place of or together with it. This substitution or addition can add more tension and complexity to the progression, leading to a more interesting and dynamic result.
| F Maj7 | C7 |
⇒
| F Maj7 | G7/G7#9 | C7 |
G7#9 Chord Function in Major and Minor Keys
G7#9 as Dominant Chord in C Major
In the key of C major, the G7 chord would be the dominant chord. The G7 chord can be coupled or substituted by a G7#9, let’s see how:
| I | ii | iii | IV | V | vi | vii |
| C Maj7 | D min7 | E min7 | F Maj7 | G7 | A min7 | Bm7b5 |
G7#9 Chord Progressions as V degree
Try playing these chord progressions to get an idea of how G7#9 functions near the dominant chord. I like to use it followed by a G7b9 but feel free to experiment.
ii V I
| ii | V | I |
| D min7 | G7#9 | G7b9
G (B, F, A#) | G (B, F, Ab) |
C Maj7 |
I IV vi V
| I | IV | vi | V |
| C Maj7 | F Maj7 | A min 7 | G7#9 | G7b9 |
I IV ii V iii vi ii V
| I | IV | ii | V | iii | vi | ii | V |
| C Maj7 | F Maj7 | D min7 | G7#9 | G7b9 | E min7 | A min7 | D min7 | G7#9 | G7b9 |
G7#9 as Dominant Chord in C minor
G7 can be found also on the V degree of the C melodic and harmonic minor scales. It’s very common to use this chord in combination with chords built on the natural minor scale or to substitute it for the G min7 chord that is present in the natural minor scale. In some context, we could use a G7#9 instead of a G7 in this position.
| i | ii | III | iv | v | VI | VII |
| C min7 | Dm7b5 | Eb Maj7 | F min7 | G min7 ⇒ G7 ⇒ G7#9 | Ab Maj7 | Bb7 |
G7#9 as V degree on Minor Scale – Chord Progressions
Try playing these chord progressions to get an idea of how G7#9 functions as the subdominant (V degree) in the key of C minor.
ii V7 i
| ii | V7 | i |
| Dm7b5 | G7#9 | G7b9 | C min7 |
i iv V7
| i | iv | V7 |
| C min7 | F min7 | G7#9 | G7b9 |
i iv VI V7
| i | iv | VI | V7 |
| C min7 | F min7 | Ab Maj7 | G7#9 | G7b9 |
Circle Progression
| i | iv | VII | III | VI | ii | V7 | i |
| C min7 | F min7 | Bb7 | Eb Maj7 | Ab Maj7 | Dm7b5 | G7#9 | G7b9 | C min7 |
G7#9 as III7 Degree in Eb Major
This is a very common substitution of dominant chords in place of minor chords. In the case of G7, we are in Eb major since the minor chord we are going to substitute is on the iii degree of the scale:
| I | ii | iii | IV | V | vi | vii |
| Eb Maj7 | F min7 | G min7 | Ab Maj7 | Bb7 | C min7 | Dm7b5 |
G7#9 as III7 degree – Chord Progressions
Try playing these chord progressions to get an idea of how G7#9 functions in this position. To understand why this substitution is possible, I suggest checking out some of the posts related to dominant 7th chords. There are different interpretations of this substitution, so it can be helpful to explore them to fully understand its potential use.
I III7 vi
| I | III7 | vi |
| Eb Maj7 | G7#9 | G7b9 | C min7 |
I III7 VI7 ii
| I | III7 | VI7 | ii |
| Eb Maj7 | G7#9 | G7b9 | C7 | F min7 |
I III7 IV VI7 ii V iii/biiiø ii/V
| I | III7 | IV | VI7 | ii | V | iii/biiiø | ii/V |
| Eb Maj7 | G7#9 | G7b9 | Ab Maj7 | C7 | F min7 | Bb7 | G min7 | Gb dim | F min7 | Bb7 |
“All of me” Progression
| I | III7 | VI7 | ii | III7 | vi | II7 | ii/V |
| Eb Maj7 | G7#9 | G7b9 | C7 | F min7 | G7#9 | G7b9 | C min7 | F7 | F min7 | Bb7 |
G7#9 as Leading Tone Chord in A minor
In the key of A minor, the G7 chord is built on the leading tone, which is the seventh note of the scale. This chord can be replaced or modulated by a G7#9, although it may not be the most ideal position for this chord. Nonetheless, it can still be a valid option in certain musical contexts.
| i | ii | III | iv | v | VI | VII |
| A min7 | Bm7b5 | C Maj7 | D min7 | E min7 | F Maj7 | G7 |
G7#9 as VII degree – Chord Progressions
i iv VII i
| i | iv | VII | i |
| A min7 | D min7 | G7#9 | G7b9 | A min7 |
i iv VII III
| i | iv | VII | III |
| A min7 | D min7 | G7#9 | G7b9 | C Maj7 |
Circle Progression
| i | iv | VII | III | VI | ii | V7 | i |
| A min7 | D min7 | G7#9 | G7b9 | C Maj7 | F Maj7 | Bm7b5 | E7 | A min7 |
Alternative G7#9 Nomenclature
- G 7+9
- G 7(#9)
- Sol 7#9
- G 7#9th
- G dom7#9
- G Dominant 7th #9
- G Dominant Seventh Sharp Ninth
Conclusion
The chord progressions and examples presented in this post provide a comprehensive overview of the most common uses of the G7#9 chord. It’s important to note, however, that many advanced harmony-related topics could not be included due to space constraints. These topics include chord progressions built on harmonic and melodic scales, modal scales, hidden tonality, secondary dominants and other chord substitutions, non-functional harmony and atonal music, modal interchange and borrowed chords, voice leading and counterpoint, chromatisms, jazz harmony…I mean, music theory is a huge topic!
Although I couldn’t cover all of these topics in my post, I encourage readers to continue exploring these areas in their own study and research. By expanding your knowledge in these advanced areas of music theory, you can gain a deeper understanding of the harmonic possibilities that exist beyond the basics presented here.