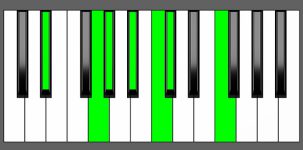
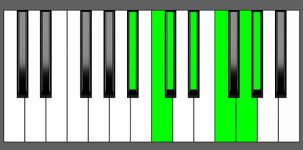
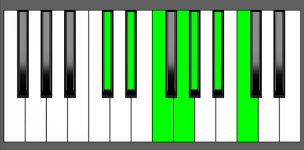
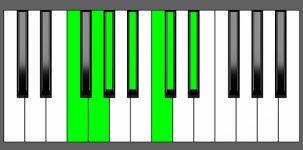
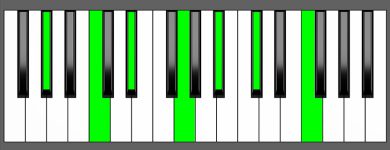
Piano Diagram of G# Maj13 in Root Position

The G# Maj13 is a chord that includes the root note G#, a major third (B#), a perfect fifth (D#), a major seventh (Fx), a major ninth (A#), an eleventh (C#) and a 13th (E#). It’s a diatonic extension of a G# Maj13 chord with an extra layer of notes (9th, 11th, and 13th).
Structure of G# Maj13
Notes |
|---|
| G#, B#, D#, Fx, A#, C#, E# |
Intervals |
|---|
| R, 3, 5, 7, 9, 11, 13 |
Playing Extended Chords on Piano
Extended chords are commonly used in piano playing, but they can be tricky to play in their entirety due to the large number of notes involved. To make these chords more manageable, pianists often omit certain notes, such as the root or the 5th. Another technique is to split the chord between both hands, playing either full or partial chords in each hand.
How to play a G# Maj13
One approach to playing the G# Maj13 chord is to begin by playing the root note G# with your left hand then, with your right hand, you can play the minor 7th note Fx, the 9th note A#, and the 13th note E#.
G# + Fx, A#, E# = G# Maj13
This will result in a simplified G# Maj13 chord that only includes the root note, major 7th, 9th, and 13th notes.
Alternatively, you can play the root note with your left hand and an inversion of the chord with the 7th note (Fx), the 3rd note (B#), and the 13th note (E#) with your right hand.
G# + Fx, B#, E# = G# Maj13
However, even when notes are omitted or split between hands, extended chords can still create complex and dense harmonies. When these chords are inverted, the resulting clusters of notes can be particularly challenging to voice effectively.
G# Maj13 Chord Inversions
The G# Maj13 chord has a total of 6 inversions:
| Root Position: | G# | B# | D# | Fx | A# | C# | E# |
| 1st Inversion: | B# | D# | Fx | G# | A# | C# | E# |
| 2nd Inversion: | D# | Fx | G# | A# | B# | C# | E# |
| 3rd Inversion: | Fx | G# | A# | B# | C# | D# | E# |
| 4th Inversion: | A# | B# | C# | D# | E# | Fx | G# |
| 5th Inversion | C# | D# | E# | Fx | G# | A# | B# |
| 6th Inversion | E# | Fx | G# | A# | B# | C# | D# |
Piano Keyboard Diagrams
Chord Inversions on Piano
Understanding chord inversions is an essential aspect of music theory as it helps to explain how chords are arranged. When playing chord inversions on a piano, it’s important to keep in mind that the diagrams used to illustrate the order of notes may not always be practical or even possible to play.
To achieve the proper chord voicings on a piano, you need to distribute the notes of the chord across various octaves and positions on the keyboard. This often means that the basic shape of the chord’s inversions shown in diagrams may not be the most convenient or comfortable way to play the chord.
While chord inversion diagrams can be useful in comprehending the structure and sequence of notes in a chord, it’s always a good idea to try out different voicings and fingerings to discover the most efficient and comfortable way to play the chord, while still maintaining its intended harmonic function and sound.
Music Theory and Harmony of G# Maj13
The G# Maj13 chord is a natural extension of the G# Maj13 chord, and it can serve as a variation or substitution for the latter.
Alternatively, it can be used as part of a modulation that resolves to a more stable G# chord.
Essentially, the G# Maj13 chord can be played in any position where the G# Maj13 chord is used, but it is particularly useful when played in combination with it. However, it’s important to note that some positions may not work as well as others when using G# Maj13 instead of G# Maj13.
Building the G# Maj13 Chord: Different Approaches
Starting from the G# Major Scale
To form a Maj13 chord, you combine the root, the major 3rd, the 5th, the major 7th, the major 9th, the 11th, and the 13th from a major scale. To build a G# Maj13, you can start with the G# Major scale:


To create a G# Maj13 chord, apply the formula R, 3, 5, 7, 9, 11, 13 in the following way:
- Begin with the Root note, which is G#.
- Select the major 3rd interval, which is B#, and add it to the chord.
- Add the 5th interval, D#.
- Add the major 7th interval, Fx.
- Add the major 9th which is A#.
- Add the 11th C#, which is a 4th interval at the higher octave.
- Lastly, add the 13th (E#) which is also a 6th at a higher octave.
By following this simple formula, you can create a 13th chord from any major scale.
by Combining Intervals
One method to create a major 13th chord is by combining specific intervals – a major 3rd, a minor 3rd, a major 3rd, a minor 3rd, again a minor 3rd, and finally a major 3rd. This is the formula:
3 + m3 + 3 + m3 + m3 + 3 = Major 13th Chords
Upon analysis of the G# Maj13 chord, we can note that:
- the interval between G# and B# is a major 3rd,
- between B# and D# is a minor 3rd,
- between D# and Fx is a major 3rd,
- between Fx and A# is a minor 3rd,
- between A# and C# there is a minor 3rd,
- and finally, between C# and E# there is a major 3rd.
by Combining Chords
Another way to build major 13th chords is by combining a major triad with a diminished 7th chord derived from its major 7th, or by merging a major 7th chord with a minor triad that is based on its second interval.
To build a G# Maj13 chord, you can blend a G# Major triad (G#, B#, D#) with an Fx dim7 chord (Fx, A#, C#, E#) or a G# Maj13 (G#, B#, D#, Fx) with an A# minor (A#, C#, E#).
G# Major + Fx dim7 = G# Maj13
or
G# Maj13 + A# min = G# Maj13
How to Use G# Maj13 in a Chord Progression
The G# Maj13 chord is essentially an extension of the G# Maj13 chord, with the addition of the 9th (A#), the 11th (C#), and the 13th (E#) note. These extra notes add a lot of dissonance and tension to the chord, which can make it tricky to use in a chord progression. Even if you leave out some of the notes, you still need to find the right voicing, because the effect of the G# Maj13 depends on how it fits in with the other chords.
In this post, we will focus just on the most common uses of the G# Maj13 chord. The tables of the major and natural minor scales below include the G# minor 7th chord, which can be substituted or complemented by a G# minor 13th chord.
It’s important to keep in mind that all these keys are considered theoretical and not commonly used in practice. This is mainly due to their complex nature, with a high number of accidentals. It’s more convenient to refer to their enharmonic equivalent keys, as they involve fewer accidentals.
on Major Scales
| Major Scales | I | ii | iii | IV | V | vi | vii |
|---|---|---|---|---|---|---|---|
| G# = Ab | AbMaj7 ⇒ AbMaj13 = G#Maj13 | Bb min7 | C min7 | Db Maj7 | Eb7 | F min7 | Gm7b5 |
| D# = Eb | Eb Maj7 | F min7 | G min7 | AbMaj7 ⇒ AbMaj13 = G#Maj13 | Bb7 | C min7 | Dm7b5 |
- Tonic chord in Ab Major as Ab Maj13
- Subdominant chord in Eb Major as Ab Maj13
on Natural minor Scales
| Minor Scales | i | ii | III | iv | v | VI | VII |
|---|---|---|---|---|---|---|---|
| E# = F | F min7 | Gm7b5 | AbMaj7 ⇒ AbMaj13 = G#Maj13 | Bb min7 | C min7 | Db Maj7 | Eb7 |
| B# = C | C min7 | Dm7b5 | EbMaj7 | F min7 | G min7 | AbMaj7 ⇒ AbMaj13 = G#Maj13 | Bb7 |
- Mediant chord in F minor as Ab Maj13
- Submediant chord in C minor as Ab Maj13
G# Maj13 as the Tonic Chord in G# Major
G# Maj13 as Subdominant Chord in D# Major
G# Maj13 as the Mediant Chord in E# Minor
G# Maj13 as the Submediant Chord in B# Minor
Alternative Names for G# Maj13 Chord
- G# j13
- G# ∆13
- G# M13
- G# ∆(13)
- G# Ma13
- G# maj13
- G# Maj13
- G# major 13
- G# Maj13(13)