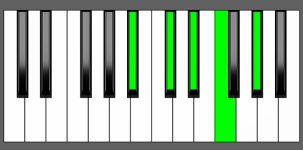
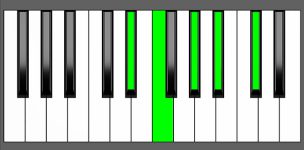
Piano Diagram of C#6/9 in Root Position

C#6/9 is a five-note chord consisting of the notes C#, E#, G#, A#, and D#. It is a major chord with an added 6th and 9th. It belongs to the chord family of 6th chords, which are “Added chords”. Keep reading to gain a deeper understanding of the music theory behind this chord.
Structure of C#6/9
Notes |
|---|
| C#, E#, G#, A#, D# |
Intervals |
|---|
| R, 3, 5, 6, 9 |
Playing Extended Chords on Piano
Extended chords are an essential part of piano playing, providing a rich and complex sound. However, playing extended chords can be challenging due to the number of notes involved. One way to manage this is by omitting certain notes, such as the root or the 5th, or by dividing the chord between both hands.
Despite these techniques, extended chords can still create dense harmonies that require careful voicing. When inverted, these chords can produce complex clusters of notes that need to be approached with skill and precision. Mastering the voicing of extended chords takes time and practice, but it’s a crucial skill for any pianist looking to expand their repertoire.
C#6/9 Chord Inversions
The C#6/9 chord has a total of 4 inversions:
| Root Position: | C# | E# | G# | A# | D# |
| 1st Inversion: | E# | G# | A# | C# | D# |
| 2nd Inversion: | G# | A# | C# | D# | E# |
| 3rd Inversion: | A# | C# | D# | E# | G# |
| 4th Inversion: | D# | E# | G# | A# | C# |
Piano Keyboard Diagrams
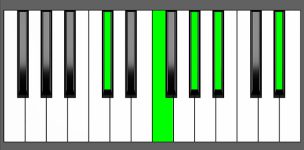
Chord Inversion on Piano
Chord inversions are a foundational concept in music theory, helping to explain how chords are built and how they fit into progressions. However, when we talk about chord inversions on a piano keyboard, it’s important to keep in mind that the diagrams we use to show the notes in an inversion might not always match up with practical playing.
In practice, pianists use different voicings and fingerings for chords, spreading the notes out across different octaves and positions on the keyboard. This means that the basic shape of a chord’s inversions as shown in diagrams might not always be the most efficient way to play the chord on a piano keyboard.
So while chord inversion diagrams can help understand the sequence of notes in a chord, they don’t always give us the best way to play the chord on a piano. It’s up to each pianist to experiment with different voicings and find the most comfortable and efficient way to play the chord while still maintaining the intended harmonic function and sound.
Music Theory and Harmony of C#6/9
Building the C#6/9 Chord: Different Approaches
Starting from the C# Major Scale
To create a 6/9 chord, you can use the Major scale as a reference by combining a Root, a 3rd, a 5th, a 6th, and a 9th.
In this case, to build a C#6/9 let’s start from the C# Major scale:


Apply the formula R, 3, 5, 6, 9 to get a C#6/9 chord:
- Select the Root note, which is C#.
- Pick the 3rd note, which is E#, and add it to the chord.
- Add the 5th note, which is G#, and include it as well.
- Now, add the 6th which is A#.
- Lastly, include the 9th note of the C# Major scale, which is a D#.
by Combining Intervals
To build a 6/9 chord, one approach is to combine specific intervals, namely a major 3rd, a minor 3rd, a major 2nd (whole-tone), and a major 3rd.
3 + m3 + 2 + 3 = 6/9 Chords
When constructing a C#6/9 chord, you can see that
- C#-E# forms a major 3rd,
- E#-G# creates a minor 3rd,
- G#-A# makes a whole-tone interval, and
- B-D# is a major 3rd.
Stacking these intervals together creates a C#6/9 chord.
How to Use C# 6/9 in a Chord Progression
Since 6/9th chords are based on major triads with a sixth and a ninth added, they can substitute the major chords built on the scale of the root. This means that we can use the C#6/9 chord in those positions on the scale where the harmonization makes a major chord.
In some cases, a 6/9 chord can be used as a dominant chord, but it is less common than its use as a tonic or subdominant chord.
The following tables illustrate the harmonization of scales that contain a C# Maj7 or a C#7 chord.
on Major Scales
G# Major is a theoretical key, so it’s more practical to refer to the key of Ab Major because it has fewer accidentals in its key signature.
| Major Scales | I | ii | iii | IV | V | vi | vii |
|---|---|---|---|---|---|---|---|
| C# | C# Maj7 ⇒ C#6/9 | D# min7 | E# min7 | F# Maj7 | G#7 | A# min7 | B#m7b5 |
| G# = Ab | Ab Maj7 | Bb min7 | C min7 | Db Maj7 ⇒ Db6/9 = C#6/9 | Eb7 | F min7 | Gm7b5 |
| F# | F# Maj7 | G# min7 | A# min7 | B Maj7 | C#7 ⇒ C#6/9 | D# min7 | E#m7b5 |
- Tonic chord in C# Major
- Subdominant chord in Ab Major as Db6/9
- Dominant chord in F# Major (less common)
on Natural minor Scales
E# minor is also a theoretical key, and for practical purposes, it’s more appropriate to refer to the key of F minor. The key of F minor shares the same pitches but is notated with fewer accidentals
| Minor Scales | i | ii | III | iv | v | VI | VII |
|---|---|---|---|---|---|---|---|
| A# | A# min7 | B#m7b5 | C# Maj7 ⇒ C#6/9 | D# min7 | E# min7 | F# Maj7 | G#7 |
| E# = F | F min7 | Gm7b5 | Ab Maj7 | Bb min7 | C min7 | Db Maj7 ⇒ Db6/9 = C#6/9 | Eb7 |
| D# | D# min7 | E#m7b5 | F# Maj7 | G# min7 | A# min7 | B Maj7 | C#7 ⇒ C#6/9 |
- Mediant chord in A# minor
- Submediant chord in F minor as Db6/9
- Dominant chord in D# minor (less common)
C#6/9 in C# Major
C#6/9 can be used instead of a C# Maj or C# Maj7 chord, which is the first chord in the harmonized C# major scale.
In a major key, the I chord (built on the first degree of the major scale) serves as the tonic chord, providing the harmonic center of the chord progression.
| I | ii | iii | IV | V | vi | vii |
| C# Maj7 ⇒ C#6/9 | D# min7 | E# min7 | F# Maj7 | G#7 | A# min7 | B#m7b5 |
C#6/9 Chord Progressions as I degree
II V I
| ii | V | I |
| D# min7 | G#7 | C#6/9 | C# Maj7 |
I IV V
| I | IV | V |
| C#6/9 | F# Maj7 | G#7 |
I V vi IV
| I | V | vi | IV |
| C#6/9 | G#7 | A# min7 | F# Maj7 |
C#6/9 in G# Major
C#6/9 Chord in F# Major
Another (uncommon) way to use the C#6/9 chord is as a substitution for the dominant chord in the F# major scale. In this case, the C#6/9 chord functions as a variation of the C#7 chord, serving as the fifth degree of the F# major scale.
When used in a ii-V-I progression, the C#6/9 chord on the fifth degree can function as the dominant chord that resolves to the first degree.
| I | ii | iii | IV | V | vi | vii |
| F# Maj7 | G# min7 | A# min7 | B Maj7 | C#7 ⇒ C#6/9 | D# min7 | E#m7b5 |
C#6/9 as V degree – Chord Progressions
I prefer resolving the C#6/9 chord to a C#7 chord within the same measure, but I encourage you to explore different options and experiment with other chord progressions to see what sounds best to you.
ii V I
| ii | V | I |
| G# min7 | C#6/9 | C#7 | F# Maj7 |
I IV vi V
| I | IV | vi | V |
| F# Maj7 | B Maj7 | D# min 7 | C#6/9 | C#7 |
I IV ii V iii vi ii V
| I | IV | ii | V | iii | vi | ii | V |
| F# Maj7 | B Maj7 | G# min7 | C#6/9 | C#7 | A# min7 | D# min7 | G# min7 | C#6/9 | C#7 |
C#6/9 in A# minor
Similarly, in the key of A# minor, the C#6/9 chord can be used as a substitute for the C# Maj7 chord as the third degree.
| i | ii | III | iv | v | VI | VII |
| A# min7 | B#m7b5 | C# Maj7 ⇒ C#6/9 | D# min7 | E# min7 | F# Maj7 | G#7 |
C#6/9 as III degree – Chord Progressions
These chord progressions show the C#6/9 chord as a substitute for the mediant (III degree) chord.
i III
| i | III |
| A# min7 | C#6/9 | C# Maj7 |
i III VII VI
| i | III | VII | VI |
| A# min7 | C#6/9 | C# Maj7 | G#7 | F# Maj7 |
Circle Progression
| i | iv | VII | III | VI | ii | V7 | i |
| A# min7 | D# min7 | G#7 | C#6/9 | C# Maj7 | F# Maj7 | B#m7b5 | E#7 | A# min7 |
C#6/9 in E# minor
C#6/9 in D# minor
Using a C#6/9 instead of a Major or Major 7th as the dominant chord is not so common but it is worth mentioning.
| i | ii | III | iv | v | VI | VII |
| D# min7 | E#m7b5 | F# Maj7 | G# min7 | A# min7 | B Maj7 | C#7 ⇒ C#6/9 |
C#6/9 as VII degree – Chord Progressions
You can try playing these chord progressions to hear how the C#6/9 chord works as a substitute for the subdominant (IV degree) or you can play it with the dominant 7th chord:
i VI VII
| i | V | VII |
| D# min7 | B Maj7 | C#6/9 | C#7 |
i v VI VII
| i | v | VI | VII |
| D# min7 | A# min7 | B Maj7 | C#6/9 | C#7 |
i III VII VI
| i | III | VII | VI |
| D# min7 | F# Maj7 | C#6/9 | C#7 | B Maj7 |
Circle Progression
| i | iv | VII | III | VI | ii | V7 | i |
| D# min7 | G# min7 | C#6/9 | C#7 | F# Maj7 | B Maj7 | E#m7b5 | A#7 | D# min7 |
Alternative Names for C#6/9
- C# 6/9
- C# 6(9)
- Do# 6/9
- C# 6/9th
- C# add6/9
Conclusion
The chord progressions and examples presented in this post provide a comprehensive overview of the most common uses of the C#6/9 chord. It’s important to note, however, that many advanced harmony-related topics could not be included due to space constraints. These topics include chord progressions built on harmonic and melodic scales, modal scales, hidden tonality, secondary dominants and other chord substitutions, non-functional harmony and atonal music, modal interchange and borrowed chords, voice leading and counterpoint, chromatisms, jazz harmony…I mean, music theory is a huge topic!
Although I couldn’t cover all of these topics in my post, I encourage readers to continue exploring these areas in their study and research. By expanding your knowledge in these advanced areas of music theory, you can gain a deeper understanding of the harmonic possibilities that exist beyond the basics presented here.