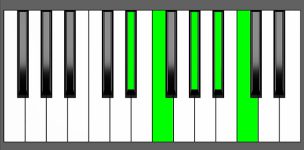
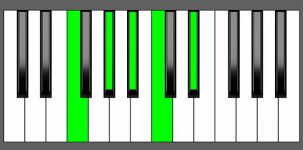
Piano Diagram of G#6/9 in Root Position

G#6/9 is a five-note chord consisting of the notes G#, B#, D#, E#, and A#. It is a major chord with an added 6th and 9th. It belongs to the chord family of 6th chords, which are “Added chords”. Keep reading to gain a deeper understanding of the music theory behind this chord.
Structure of G#6/9
Notes |
|---|
| G#, B#, D#, E#, A# |
Intervals |
|---|
| R, 3, 5, 6, 9 |
Playing Extended Chords on Piano
Extended chords are an essential part of piano playing, providing a rich and complex sound. However, playing extended chords can be challenging due to the number of notes involved. One way to manage this is by omitting certain notes, such as the root or the 5th, or by dividing the chord between both hands.
Despite these techniques, extended chords can still create dense harmonies that require careful voicing. When inverted, these chords can produce complex clusters of notes that need to be approached with skill and precision. Mastering the voicing of extended chords takes time and practice, but it’s a crucial skill for any pianist looking to expand their repertoire.
G#6/9 Chord Inversions
The G#6/9 chord has a total of 4 inversions:
| Root Position: | G# | B# | D# | E# | A# |
| 1st Inversion: | B# | D# | E# | G# | A# |
| 2nd Inversion: | D# | E# | G# | A# | B# |
| 3rd Inversion: | E# | G# | A# | B# | D# |
| 4th Inversion: | A# | B# | D# | E# | G# |
Piano Keyboard Diagrams
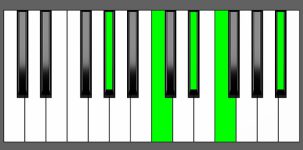
Chord Inversion on Piano
Chord inversions are a foundational concept in music theory, helping to explain how chords are built and how they fit into progressions. However, when we talk about chord inversions on a piano keyboard, it’s important to keep in mind that the diagrams we use to show the notes in an inversion might not always match up with practical playing.
In practice, pianists use different voicings and fingerings for chords, spreading the notes out across different octaves and positions on the keyboard. This means that the basic shape of a chord’s inversions as shown in diagrams might not always be the most efficient way to play the chord on a piano keyboard.
So while chord inversion diagrams can help understand the sequence of notes in a chord, they don’t always give us the best way to play the chord on a piano. It’s up to each pianist to experiment with different voicings and find the most comfortable and efficient way to play the chord while still maintaining the intended harmonic function and sound.
Music Theory and Harmony of G#6/9
Building the G#6/9 Chord: Different Approaches
Starting from the G# Major Scale
To create a 6/9 chord, you can use the Major scale as a reference by combining a Root, a 3rd, a 5th, a 6th, and a 9th.
In this case, to build a G#6/9 let’s start from the G# Major scale:


Apply the formula R, 3, 5, 6, 9 to get a G#6/9 chord:
- Select the Root note, which is G#.
- Pick the 3rd note, which is B#, and add it to the chord.
- Add the 5th note, which is D#, and include it as well.
- Now, add the 6th which is E#.
- Lastly, include the 9th note of the G# Major scale, which is an A#.
by Combining Intervals
To build a 6/9 chord, one approach is to combine specific intervals, namely a major 3rd, a minor 3rd, a major 2nd (whole-tone), and a major 3rd.
3 + m3 + 2 + 3 = 6/9 Chords
When constructing a G#6/9 chord, you can see that
- G#-B# forms a major 3rd,
- B#-D# creates a minor 3rd,
- D#-E# makes a whole-tone interval, and
- F#-A# is a major 3rd.
Stacking these intervals together creates a G#6/9 chord.
How to Use G# 6/9 in a Chord Progression
Since 6/9th chords are based on major triads with a sixth and a ninth added, they can substitute the major chords built on the scale of the root. This means that we can use the G#6/9 chord in those positions on the scale where the harmonization makes a major chord.
In some cases, a 6/9 chord can be used as a dominant chord, but it is less common than its use as a tonic or subdominant chord.
The following tables illustrate the harmonization of scales that contain a G# Maj7 or a G#7 chord.
on Major Scales
The chords G#Maj7 and G#7 are typically found in theoretical keys, making it more practical to refer to their equivalent keys. While G#7 is present in the key of C#, it’s worth noting that the use of a 6/9 chord as a dominant chord in this context is uncommon.
| Major Scales | I | ii | iii | IV | V | vi | vii |
|---|---|---|---|---|---|---|---|
| G# = Ab | Ab Maj7 ⇒ Ab6/9 = G#6/9 | Bb min7 | C min7 | Db Maj7 | Eb7 | F min7 | Gm7b5 |
| D# = Eb | Eb Maj7 | F min7 | G min7 | Ab Maj7 ⇒ Ab6/9 = G#6/9 | Bb7 | C min7 | Dm7b5 |
| C# | C# Maj7 | D# min7 | E# min7 | F# Maj7 | G#7 ⇒ G#6/9 | A# min7 | B#m7b5 |
- Tonic chord in Ab Major as Ab6/9
- Subdominant chord in Eb Major as Ab6/9
- Dominant chord in C# Major (less common)
on Natural minor Scales
Same goes for the theoretical minor keys (E# and B#); we will refer to their equivalent keys.
| Minor Scales | i | ii | III | iv | v | VI | VII |
|---|---|---|---|---|---|---|---|
| E# = F | F min7 | Gm7b5 | Ab Maj7 ⇒ Ab6/9 = G#6/9 | Bb min7 | C min7 | Db Maj7 | Eb7 |
| B# = C | C min7 | Dm7b5 | Eb Maj7 | F min7 | G min7 | Ab Maj7 ⇒ Ab6/9 = G#6/9 | Bb7 |
| A# | A# min7 | B#m7b5 | C# Maj7 | D# min7 | E# min7 | F# Maj7 | G#7 ⇒ G#6/9 |
- Mediant chord in F minor as Ab6/9
- Submediant chord in C minor as Ab6/9
- Dominant chord in A# minor (less common)
G#6/9 in G# Major
G#6/9 in D# Major
G#6/9 Chord in C# Major
Another (uncommon) way to use the G#6/9 chord is as a substitution for the dominant chord in the C# major scale. In this case, the G#6/9 chord functions as a variation of the G#7 chord, serving as the fifth degree of the C# major scale.
When used in a ii-V-I progression, the G#6/9 chord on the fifth degree can function as the dominant chord that resolves to the first degree.
| I | ii | iii | IV | V | vi | vii |
| C# Maj7 | D# min7 | E# min7 | F# Maj7 | G#7 ⇒ G#6/9 | A# min7 | B#m7b5 |
G#6/9 as V degree – Chord Progressions
I prefer resolving the G#6/9 chord to a G#7 chord within the same measure, but I encourage you to explore different options and experiment with other chord progressions to see what sounds best to you.
ii V I
| ii | V | I |
| D# min7 | G#6/9 | G#7 | C# Maj7 |
I IV vi V
| I | IV | vi | V |
| C# Maj7 | F# Maj7 | A# min 7 | G#6/9 | G#7 |
I IV ii V iii vi ii V
| I | IV | ii | V | iii | vi | ii | V |
| C# Maj7 | F# Maj7 | D# min7 | G#6/9 | G#7 | E# min7 | A# min7 | D# min7 | G#6/9 | G#7 |
G#6/9 in E# minor
G#6/9 in B# minor
G#6/9 in A# minor
Using a G#6/9 instead of a Major or Major 7th as the dominant chord is not so common but it is worth mentioning.
| i | ii | III | iv | v | VI | VII |
| A# min7 | B#m7b5 | C# Maj7 | D# min7 | E# min7 | F# Maj7 | G#7 ⇒ G#6/9 |
G#6/9 as VII degree – Chord Progressions
You can try playing these chord progressions to hear how the G#6/9 chord works as a substitute for the subdominant (IV degree) or you can play it with the dominant 7th chord:
i VI VII
| i | V | VII |
| A# min7 | F# Maj7 | G#6/9 | G#7 |
i v VI VII
| i | v | VI | VII |
| A# min7 | E# min7 | F# Maj7 | G#6/9 | G#7 |
i III VII VI
| i | III | VII | VI |
| A# min7 | C# Maj7 | G#6/9 | G#7 | F# Maj7 |
Circle Progression
| i | iv | VII | III | VI | ii | V7 | i |
| A# min7 | D# min7 | G#6/9 | G#7 | C# Maj7 | F# Maj7 | B#m7b5 | E#7 | A# min7 |
Alternative Names for G#6/9
- G# 6/9
- G# 6(9)
- Sol# 6/9
- G# 6/9th
- G# add6/9