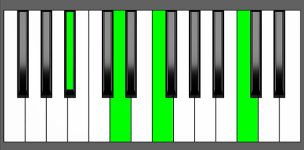
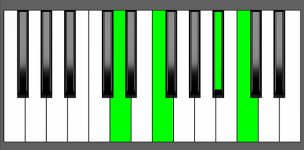
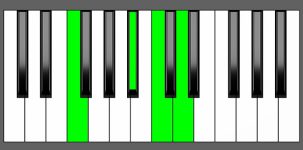
Piano Diagram of A# add9 in Root Position
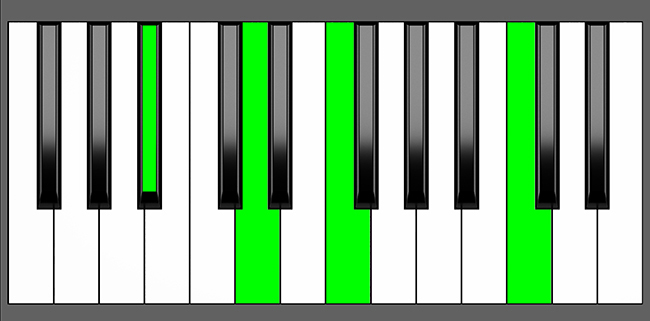
To form an A# add9 chord, you simply include a 9th note (B#) to an A# Major chord (A#, Cx, E#). Such chords are referred to as added tone chords as they involve the addition of supplementary intervals to a triad. The A# add9 chord is distinct from the A#9 chord because it doesn’t have a 7th, whereas the A#9 chord includes the 7th note. Continue reading to discover additional information about the fundamentals of added tone chords and their applications in music.
Structure of A# add9
Notes |
|---|
| A#, Cx, E#, B# |
Intervals |
|---|
| R, 3, 5, 9 |
Playing Extended Chords on Piano
Extended chords can be difficult to play in their entirety on the piano due to the large number of notes involved or the distance between intervals like in this case. To simplify these chords, pianists often omit certain notes (usually the Root or the fifth) or split the chord between both hands. However, even with these simplifications, extended chords can create complex and dense harmonies, making voicing a challenging task.
A# add9 Chord Inversions
A# add9 chord has a total of 3 inversions:
| Root Position: | A# | Cx | E# | B# |
| 1st Inversion: | Cx | E# | A# | B# |
| 2nd Inversion: | E# | A# | B# | Cx |
| 3rd Inversion: | B# | Cx | E# | A# |
Piano Keyboard Diagrams
Chord Inversions on Piano
Chord inversions are a crucial concept in music theory as they allow for a greater understanding of how chords are constructed and how they can be used in progressions.
However, it’s important to note that the diagrams depicting the sequence of notes in a chord inversion on a piano keyboard may not always translate to practical playing.
This is because proper chord voicings involve distributing the notes of the chord across different octaves and positions on the keyboard, which may differ from the basic shape of the chord’s inversions.
Therefore, while chord inversion diagrams help understand the structure and sequence of notes in a chord, they may not always be the most efficient way to play the chord on a piano keyboard.
Music Theory and Harmony of A# Add 9
Building the A# add9 Chord: Different Approaches
Starting from the A# Major Scale:
To build an Add 9 chord, begin by using the Major scale as a reference and selecting the Root, 3rd, 5th, and 9th notes.


Here are the steps to get the A# add9 chord using the formula R, 3, 5, 9:
- Begin with the Root note, which is A#.
- Add the 3rd note, which is Cx.
- Include the 5th note, which is E#.
- Finally, add the 9th note, which is B#.
by Combining Intervals:
Another approach to building an Add 9 chord involves combining particular intervals, such as a major 3rd, minor 3rd, and perfect 5th.
3 + m3 + 5 = add9 chords
For example, to create an A# add9 chord, you can layer
- A#-Cx (a major 3rd),
- Cx-E# (a minor 3rd),
- and E#-B# (a perfect 5th) on top of each other.
How to Use A# add9 in a Chord Progression
In music theory, the concept of harmonic function refers to the role a chord plays in a musical composition. A stable harmonic function is associated with a chord that provides a sense of rest or resolution, while a dominant harmonic function creates a sense of tension or instability that often leads to a resolution to a stable chord.
The harmonic function of an A# add9 chord is not fixed and can vary based on the surrounding harmonic context and the musical composition. For instance, when an A# add9 chord follows a dominant chord like E#7, it functions as a stable chord that resolves the preceding tension.
However, in other situations, such as in a chord progression in the key of D# major, the A# add9 chord can serve as a dominant chord.
It is helpful to explore which scales and degrees include an A# Maj7 or A#7 chord, which can potentially be substituted with an A# add9 chord.
on Major Scales
In this case, the A# Maj7 or A#7 chords are found solely in theoretical major keys. Consequently, it is more practical to reference their enharmonic equivalent keys.
| Major Scales | I | ii | iii | IV | V | vi | vii |
|---|---|---|---|---|---|---|---|
| A# = Bb | Bb Maj7 ⇒ Bb add9 = A# add9 | C min7 | D min7 | Eb Maj7 | F7 | G min7 | Am7b5 |
| E# = F | F Maj7 | G min7 | A min7 | Bb Maj7 ⇒ Bb add9 = A# add9 | C7 | D min7 | Em7b5 |
| D# = Eb | Eb Maj7 | F min7 | G min7 | Ab Maj7 | Bb7 ⇒ Bb add9 = A# add9 | C min7 | Dm7b5 |
- Tonic chord in Bb Major as Bb add9
- Subdominant chord in F Major as Bb add9
- Dominant chord in Eb Major as Bb add9
on Natural minor Scales
As before, we will refer to the equivalent keys as the A# Maj7 or A#7 chords are present exclusively in theoretical minor keys.
| Minor Scales | i | ii | III | iv | v | VI | VII |
|---|---|---|---|---|---|---|---|
| Fx = G | G min7 | Am7b5 | Bb Maj7 ⇒ Bb add9 = A# add9 | C min7 | D min7 | Eb Maj7 | F7 |
| Cx = D | D min7 | Em7b5 | F Maj7 | G min7 | A min7 | Bb Maj7 ⇒ Bb add9 = A# add9 | C7 |
| B# = C | C min7 | Dm7b5 | Eb Maj7 | F min7 | G min7 | Ab Maj7 | Bb7 ⇒ Bb add9 = A# add9 |
- Mediant chord in G minor as Bb add9
- Submediant chord in D minor as Bb add9
- Leading tone chord in C minor as Bb add9
A# add9 in A# Major
A# add9 in E# Major
A# add9 in D# Major
A# add9 in Fx minor
A# add9 in Cx minor
A# add9 in B# minor
Alternative Names for A# add9 Chord
- A# add9
- La# add9
- A# (add9)
- A# add(9)
- A# add 9th